1) Comparateurs de tension simple et double.
A) Réponse d'un comparateur simple à divers
signaux
L'A.O. est supposé idéal ; la tension de sortie
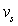 est limitée
par la saturation aux valeurs extrêmes
est limitée
par la saturation aux valeurs extrêmes 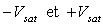 .
On donne
.
On donne 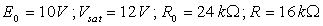
|
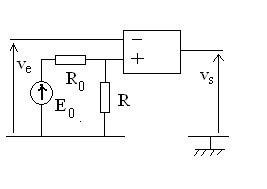
A)1) La tension d'entrée
A)2) La tension d'entrée est un signal
triangulaire symétrique de période T et d'amplitude
6 V . Représenter en le justifiant le graphe
Déterminer le rapport des durées des niveaux haut et bas. |
|
A)3) La tension d'entrée est un signal sinusoïdal
de période T : 
A)4) Comment sont modifiés les résultats
précédents si on permute les entrées 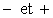 -
dans le montage étudié ?
-
dans le montage étudié ?
A)5) La source de tension auxiliaire a maintenant une
faible amplitude 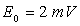 ,
l'A.O. n'est plus idéal et a un gain
,
l'A.O. n'est plus idéal et a un gain  .
Déterminer la tension d'entrée limite qui donne une saturation
négative.
.
Déterminer la tension d'entrée limite qui donne une saturation
négative.
B) Comparateur double
|
On applique une tension continue
On donne
Tracer la caractéristique
|

|
2)
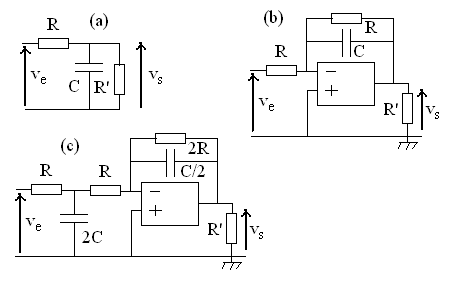
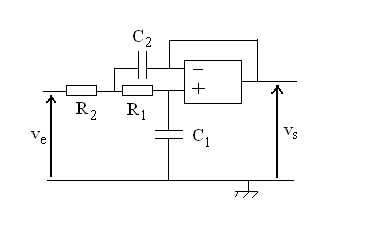
2)1) Calculer la fonction de transfert 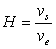 du circuit (a).
du circuit (a).
On note 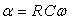 .
Etudier les cas
.
Etudier les cas  .
.
2)2) Calculer la fonction de transfert du circuit (b).
R' étant la résistance de charge, quel est l'avantage du
circuit (b) par rapport au circuit (a).
2)3) On étudie le circuit (c) : calculer sa fonction
de transfert et représenter les diagrammes de Bode des circuits (b) et
(c). Comparer.
(Les A.O. sont supposés parfaits)
|
3) L'A.O. est parfait et fonctionne en régime
linéaire.
3)1) Déterminer, en régime sinusoïdal,
la fonction de transfert
3)2) Le dipôle d'impédance Z
correspond à une résistance R en parallèle
avec un condensateur de capacité C, le dipôle d'impédance
Z' à une résistance R en série avec
un condensateur de capacité C.
A quelle condition le montage proposé constitue t'il un montage déphaseur ? |

|
| Réponse
31 | Réponse
32 |
|
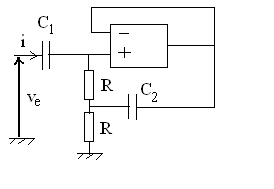
4) Montrer que ce circuit
est équivalent à un circuit R,
L, C série.
Calculer la fréquence de résonance, le
facteur de qualité.
Conclusions.
|
|
| Réponse
4 |
5)
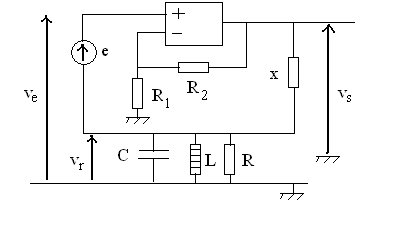
5)1) On se place en régime sinusoïdal forcé,
l'A.O. fonctionnant en régime linéaire.
Déterminer les rapports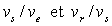 .
.
Déterminer les rapports
5)2) On supprime la source e. Quelle valeur faut-il
donner à x pour obtenir des oscillations ?
Quelle est la pulsation correspondante ?
Quelle est la pulsation correspondante ?
| Réponse
51 | Réponse
52 |
6)
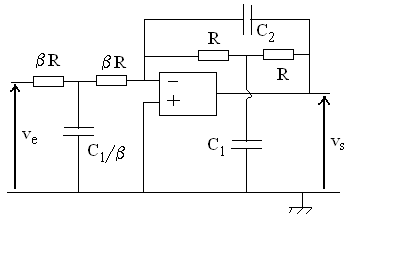
L'A.O. est parfait.
6)1) Déterminer la fonction de transfert en régime
sinusoïdal : 
6)2) Donner la réponse à un échelon
de tension : 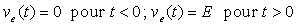 .
.
Discuter la stabilité d'un tel système. On posera .
.
Discuter la stabilité d'un tel système. On posera
| Réponse
61 | Réponse
62 |
7)
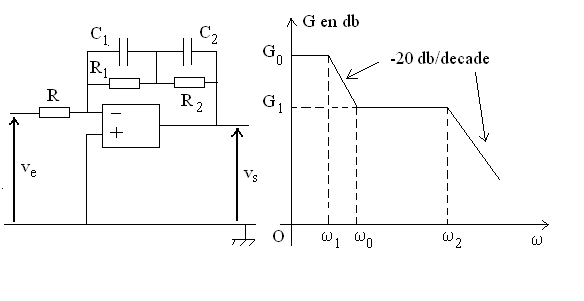
On suppose que le système fonctionne en régime
linéaire sinusoïdal. On enregistre le diagramme de Bode donnant


7)1) Justifier, par le raisonnement les grandes lignes
du diagramme données sur la figure ci-dessus.
7)2) Trouver la fonction 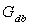 et tracer le diagramme.
et tracer le diagramme.
| Réponse
71 | Réponse
72 |
8)

8)1) Déterminer l'impédance Z du
dipôle D pour que la fonction de transfert 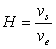 soit nulle.
soit nulle.
8)2) Le dipôle D correspond
au montage à droite ci-dessus.
8)2)a) Déterminer son impédance d'entrée Z'.
8)2)b) Peut-on réaliser la condition imposée en 1) ?
Tracer alors la courbe donnant .
.
8)2)a) Déterminer son impédance d'entrée Z'.
8)2)b) Peut-on réaliser la condition imposée en 1) ?
Tracer alors la courbe donnant
 .
.
9)
9)1) Montrer que la fonction de transfert peut se mettre
sous la forme :


Déterminer les valeurs de 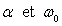 .
.
9)2) On veut que 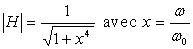 .
.
Quelle valeur faut-il donner à a pour qu'il en soit ainsi ? Quel est l'intérêt d'un tel dispositif ?
Quelle valeur faut-il donner à a pour qu'il en soit ainsi ? Quel est l'intérêt d'un tel dispositif ?
9)3) On associe deux montages, de même nature
que le précédent, caractérisés par les couples 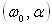 pour le premier et
pour le premier et  pour le second.
pour le second.
Quelles relations doivent vérifier les coefficients a et a' pour que le montage ainsi obtenu corresponde à une fonction de transfert telle que :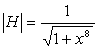 .
.
Quelles relations doivent vérifier les coefficients a et a' pour que le montage ainsi obtenu corresponde à une fonction de transfert telle que :
10) Comportement fréquentiel d'un
système bouclé
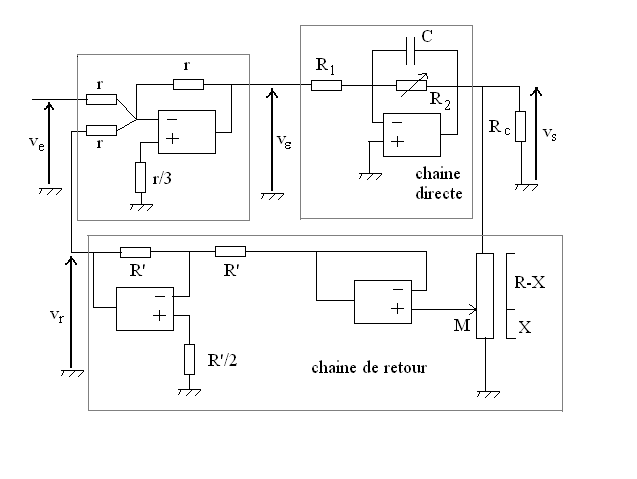
On considère le système bouclé schématisé
ci-dessous. Les quatre amplificateurs opérationnels utilisés sont
supposés parfaits et en fonctionnement linéaire.
10)1) Etablir la relation entre 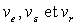 .
Quel est le rôle du module encadré en haut, à gauche ?
.
Quel est le rôle du module encadré en haut, à gauche ?
10)2)a) Exprimer la fonction de transfert complexe 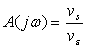 du filtre constituant la chaîne directe.
du filtre constituant la chaîne directe.
10)2)b) En déduire la pulsation de coupure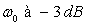 et le gain
et le gain 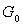 en
bande passante de la chaîne directe.
en
bande passante de la chaîne directe.
10)2)b) En déduire la pulsation de coupure
10)3) Exprimer la fonction de transfert 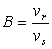 de la chaîne de retour en fonction de la résistance totale R
du rhéostat et de la résistance X variable suivant la position
du curseur M.
de la chaîne de retour en fonction de la résistance totale R
du rhéostat et de la résistance X variable suivant la position
du curseur M.
10)4)a) Exprimer la fonction de transfert complexe 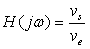 du système bouclé.
du système bouclé.
10)4)b) En déduire la pulsation de coupure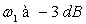 et le gain
et le gain 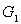 en
bande passante du système bouclé.
en
bande passante du système bouclé.
10)4)c) Comparer les produits .
.
10)4)b) En déduire la pulsation de coupure
10)4)c) Comparer les produits
| Réponse
101 | Réponse
102a | Réponse
102b | Réponse
103 | Réponse
104a | Réponse
104b | Réponse
104c |
11)
Les amplificateurs opérationnels utilisés sont
idéaux et fonctionnent en régime linéaire.
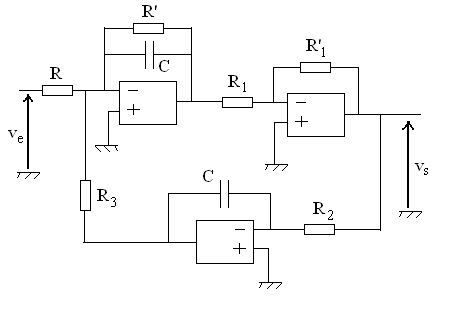
11)1) Calculer, en régime sinusoïdal établi,
la fonction de transfert  .
.
En déduire la nature du montage et donner ses caractéristiques
en prenant les valeurs :
On tracera la courbe représentant 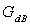 en fonction de
en fonction de 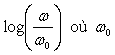 est une pulsation
à préciser.
est une pulsation
à préciser.
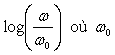 est une pulsation
à préciser.
est une pulsation
à préciser.
11)2) Quelle est la réponse du circuit à
un signal carré de valeur moyenne nulle, d'amplitude 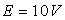 et de fréquence
et de fréquence  .
.
| Réponse
111 | Réponse
112 |
12)
|
Les amplificateurs utilisés sont idéaux.
12)1) Montrer que l'on peut écrire
Quel rôle un tel circuit peut-il jouer ?
|

|
|
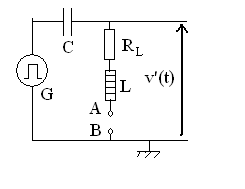
12)2) On insère le circuit ci-dessus dans
un circuit
On observe la tension 
- Calculer la résistance critique
|
|
- Montrer que, pour une valeur 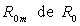 que l'on calculera, on supprime l'amortissement dans le circuit ; d'où
vient l'énergie dissipée dans les conducteurs ohmiques.
que l'on calculera, on supprime l'amortissement dans le circuit ; d'où
vient l'énergie dissipée dans les conducteurs ohmiques.
| Réponse
121 | Réponse
122 |
13)
|
13)1) Calculer les impédances complexes
En déduire le rapport
|
|
|
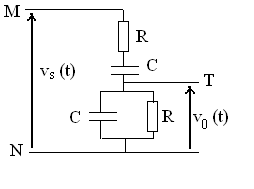
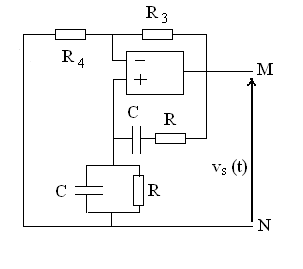
13)2) l'amplificateur opérationnel est
idéal.
- Montrer que si
- Indiquer ce qui compense alors les perte ohmiques,
- Comment le signal de sortie peut-il prendre naissance
?
|
|
| Réponse
131 | Réponse
132 |
14)
|
|
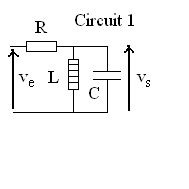
Circuit 1 : Pour quelle pulsation w
, la valeur du gain est-elle maximale ?
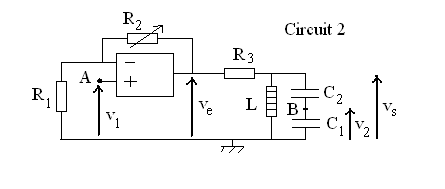
Circuit 2
- Etablir, dans le cadre d'un fonctionnement de l'A.O. en régime linéaire, la fonction de transfert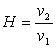 . Etudier
. Etudier 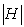 .
.
- On relie B à A. Quelle est, en régime linéaire, l'équation différentielle vérifiée par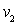 ? Qu'observe t-on suivant les valeurs de
? Qu'observe t-on suivant les valeurs de 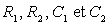 .
.
- Etablir, dans le cadre d'un fonctionnement de l'A.O. en régime linéaire, la fonction de transfert
- On relie B à A. Quelle est, en régime linéaire, l'équation différentielle vérifiée par
| Réponse
14 |
|
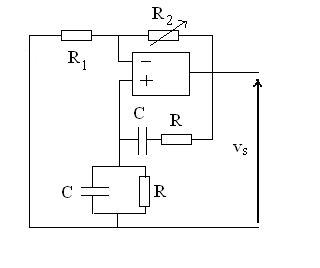
15)
Etudier le fonctionnement de ce circuit.
Que se passe t'il pour :
|
|
| Réponse
15 |
|
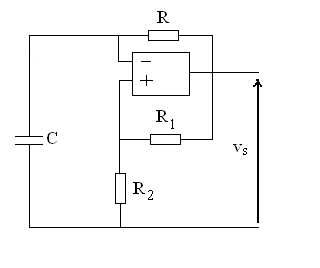
16)
Etudier le fonctionnement de ce circuit.
|
|